Popper versus Tukey and the Battle for the Heart of Statistical Data Analysis
In which the author attempts to rehabilitate the reputation of exploratory data analysis and recommends Bayesian machine learning for that purpose
The late, great Norm MacDonald had a recurring bit on his podcast where his trusty sidekick and expert stooge Adam Eget earnestly asks the guest “Where do you get your ideas from?” Veteran entertainers, like David Letterman and Adam Sandler, immediately get the joke and respond only with a smirk. It’s an inside joke: it’s a question that they are all asked constantly and which has no very good answer. It’s a question they hate to get, in other words, so when one of their own asks it, you know they are trolling.
Alas, it’s basically the question I’ve been pondering lately, except not about comedy, but about science. As a statistics professor, a core chunk of what I teach is hypothesis testing. As a group of professional scolds, statisticians are quick to remind everyone that there are Right and Wrong ways to use data to test your hypotheses. There’s a whole intellectual edifice built up around the idea that there are rules we ought to follow so that we don’t trick ourselves into believing theories that are actually wrong. It’s a nice system, all things told, but it really only works if we have a ready supply of hypotheses at hand. Statisticians, for the most part, are conspicuously mute on this topic.
There’s a hint of a paradox here, because supposedly there are Right and Wrong ways to use our data and scrutinizing the data in order to dream up explanations for the patterns we see is certainly not the Right way, according to the textbook orthodoxy. And yet, if our ideas (hypotheses, theories, etc) don’t come from data, how could they possibly explain anything about the actual world we live in? Dumb luck?
Karl Popper
This friction between data for ideation and data for theory testing actually predates the widespread adoption of the hypothesis testing framework and is explored in great depth in the work of philosopher Karl Popper (as well as his critics), particularly his 1959 book The Logic of Scientific Discovery (translated by Popper from an earlier German-language book of his from 1934). One of the major goals of Popper’s book was to develop a theory of “demarcation” which would allow us to separate scientific inquiries from nonscientific ones. The button-down hypothesis testing stuff is Science, with a capital S, and the hypothesis formulation is groping or stumbling around in the dark.
Lest you think I’m exaggerating, let me quote Daniel Lakens, a well-respected modern day Popperian (emphasis added):
“External replication often reveals that we were wrong…and the only approach we know to discover how we were wrong is to stumble across it.”
And, “If you show you have achieved [correct predictions], that is where we hand out awards. Not for the exploration part. That is just a first simple necessary step. The easy, albeit essential, first step is not what should be impressive.”
He goes on to clarify that “Exploratory just means you cannot control error rates of claims.”
Naturally, I find this approach misguided. Categorically calling anything that does not control error rates “exploration” is a mistake, I feel. It’s like saying “anything that is not classically composed music is noise, therefore jazz must be easy, just a matter of stumbling upon any old notes.” This is not how any scientist I know thinks about their work. Exploration can, and should, be much more directed than that, even if it doesn’t control error rates.
Meanwhile, as Lakens is out there denigrating the creative (yuck) side of science, the philosophers have more or less moved on. It turns out that the theory of demarcation is devilishly hard to defend and modern philosophers of science basically acknowledge that and have turned their attention to other problems. (Take the neglect of an idea by professional philosophers for what you will.) At root, the difficulty is that the line between a theory and an observation is surprisingly blurry. From the Internet Encyclopedia of Philosophy:
“Popper’s proposed criterion of demarcation […] holds that scientific theories must allow for the deduction of basic sentences whose truth or falsity can be ascertained by appropriately located observers. If, contrary to Popper’s account, there is no distinct category of basic sentences within actual scientific practice, then his proposed method for distinguishing science from non-science fails.”
Modern acolytes of Popper, particularly in the social, behavioral, and health sciences, side-step this objection by simply elevating everything to the level of a theory. These fields have settled for verification of “findings”, deploying the apparatus of hypothesis testing for this purpose and proceeding to call it science because it is “falsifiable” in the narrow sense of being able to be rejected via a hypothesis test. (Popper himself conspicuously does not write about hypothesis testing, despite it being developed squarely during his professional lifetime.)
In a phrase (and painting with a rhetorically broad brush) much of contemporary psychology would have us believe that it is enough to show that some association is true without any manifest interest in why it might true. This vantage point has its clearest exemplification in the modern business of Online Experiments where, say, different colored web page buttons are “scientifically tested” against each other to see which leads to higher online sales.
It’s worth taking a look at the sleight of hand that underlies this move from theories to mere findings. If I have a data set and I observe that in my data there is a strong association between the color of the button and the frequency with which users click the button, that’s pretty uncontroversially a “basic fact” in Popper’s terminology. What requires “testing”, in the statistical sense, is whether or not this correlation persists if we looked at larger or different groups of users. Whether or not this pattern generalizes does not (in my opinion) constitutes a scientific theory in any full-blooded sense of the term, but because it is falsifiable (subject to assumptions about the sampling frame and other details), it counts as scientific by some weak definition. From this perspective, all it takes to be scientific is to have statistical control of the error rate of our claims. And, moreover, this is the only kind of procedure that we are licensed to use if we are to call ourselves scientists. It is an empty suit caricature of science.
To recap, maybe it’s okay to call A/B testing scientific inasmuch as it employs an uninspired form of falsifiability. But we must recognize that it’s an impoverished form of science. Not just anything should count as science just because it is falsifiable. (Sabine Hossenfelder has repeatedly made this same point about flimsy justifications for building ever-larger particle colliders.) Conversely, maybe you don’t want to call data analysis methods that aren’t falsifiable (in either the broader sense or narrower sense of having control of error rates) Science (capital S), but surely there are better and worse ways to plumb our data for ideas — and surely not plumbing them at all just because we cannot guarantee error control is the dumbest possible way to do this.
Which brings me to John Tukey. A giant of contemporary science, Tukey was responsible for many brilliant ideas that we still use today. He coined the word “bit”. He invented (or reinvented, after Gauss hid it in a desk drawer) the fast Fourier transform. He gave us the witticism: “Far better an approximate answer to the right question, which is often vague, than an exact answer to the wrong question, which can always be made precise.” He also has a number of well-known statistical tests named after him.
But for the purposes of this essay, Tukey’s big idea was Exploratory Data Analysis (EDA). In 1977, Tukey published a book of that title, which is today remembered as an early contribution to statistical graphics. It introduced the box-and-whisker plot! Tukey championed EDA as a collection of techniques to facilitate the formulation of hypotheses that could lead to new data collection and experiments. It’s the answer to the Eget-esque question: where do scientists get their ideas from?
Tukey was expressly interested in nontrivial data analysis procedures that could be used to generate hypotheses to fuel Popper’s falsifiability game, to stock the shelves with hypotheses for our trusty t-tests to operate upon.
Notably, Tukey worked on many real scientific problems — far more than Popper did. He had first-hand knowledge of where our theories come from and the answer — obviously! — is data. If analyzing our data in a non-error-controlled way is frowned upon, we are that much worse off in terms of finding interesting theories to test. Right?
Not everyone sees it that way. And I think I know why — it’s because the professional scientific culture is expecting us to report the results of our labors and when issuing these report we want to report results (“findings”) rather than conjectures. In most cases our findings won’t be taken seriously unless they are corroborated with a formal statistical test. So we end up with a situation where, to the extent that you’ve done some sort of exploratory analysis, you pretend that you didn’t and then report the results of the t-test, which has the establishment’s blessings. (Ed Leamer talked about this dilemma in the memorable, and memorably-titled, paper “Let’s Take the Con Out of Econometrics”.) Conversely, we have people whose results don’t rise to the level of statistical significance, but who still find the result interesting or suggestive scientifically who end up skirting the rules and describing things as “nearly significant” or “approaching significance” — which they then get pilloried for in social media by the Righteous Gatekeepers (see screenshot).
This state of affairs is obviously undesirable. The testing purists propose to fix it by demanding pre-registration and formal replication and scorning scientists who do “mere” EDA. On the one hand, this is fine for confirmatory analysis, although I think it would lead to more Leamer-style evasion. But for exploratory analysis, it isn’t so clear that pre-registration is even possible. This, I claim, is a big part of why scientists are inclined (persistently!) to mis-use statistical tests.
Science works best when it is iterative. That is, we learn most about the world when our experiments and observations build on and reinforce (or contradict) one another. The stringent error-control purism really doesn’t encourage this at all, simply because falsifiability alone is a horribly weak requirement. It is why after decades of rigorous A/B testing for online experiments we are no closer to a theory of online consumer behavior.
Of course, throwing out statistical standards wholesale doesn’t solve the problem either. Tukey recognized all of this decades and decades ago. He was perfectly explicit that EDA shouldn’t be done on the same data that was then used for a subsequent confirmatory analysis (a la Leamer’s essay). Lots of introductory textbooks get this point wrong, suggesting that EDA is the first step in any data analysis. Making basic plots and acknowledging missing data and reformatting as necessary should be considered “prepatory analysis” rather than “exploratory”, and too many texts do not make this critical distinction.
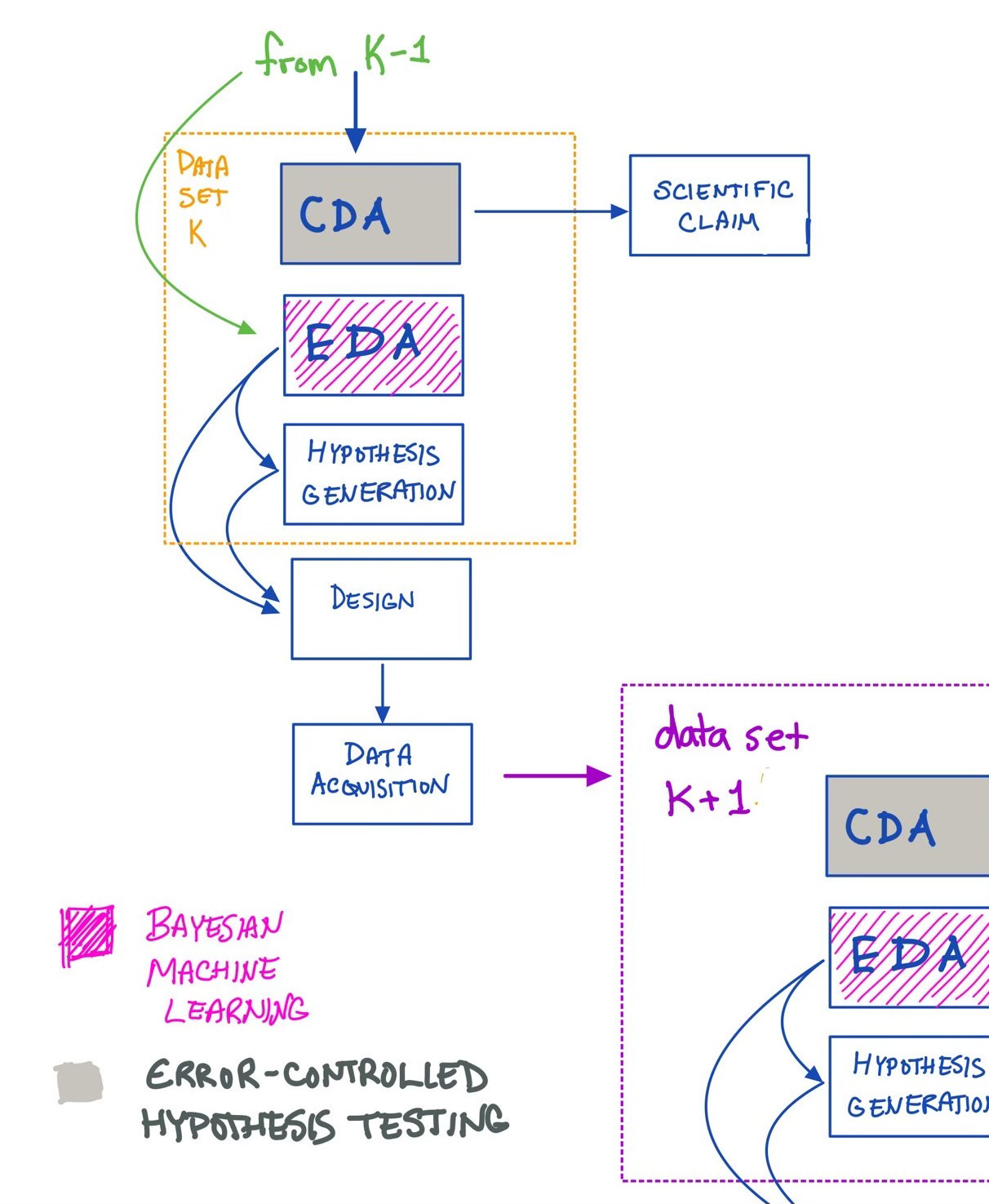
In any case, explicitly embracing iterative science solves many problems. Confirmatory analysis (orthodox error-controlled hypothesis testing) should be done on a data set for one set of questions (arising, presumably, from a previous EDA on an earlier data set). For these questions, pre-registration and replication attempts are welcome! But that data has more life in it yet — that same data can then be used for a subsequent EDA, which would inform a subsequent CDA of yet a third distinct data set. EDA should come after CDA on a given data set, but before CDA on subsequent data sets. Ideally, a public record of all of this would be kept somewhere for later cross-referencing.
Perhaps a concrete example (or two) will make my case better than abstract arguments.
You may have read something recently about the non-profit research organization Every Cure, which has been reported on in the New York Times and in dozens of social media posts and popular health and science podcasts. The story of Dr. David Fajgenbaum’s — Every Cure’s mastermind — bears on the present discussion. The high level version is that after being diagnosed with an often-fatal, treatment-resistant, rare condition called “idiopathic Castleman’s disease” Dr. Fajgenbaum set out to find an off-label drug to cure his disease and — miraculously — he succeeded. The drug he found was called sirolimus and he didn’t find it by sheer trial and error.
Sirolimus (also called rapamune) was FDA-approved in 1999 to help prevent host rejection after organ transplantation. It works by inhibiting a biological process referred to as the “mTOR pathway” (which stands for “mammalian target for rapamycin”). This “mechanism of action” is what tipped Fajgenbaum off that sirolimus might work. From extensive self-testing — performing experiments on his own lymph node tissues and blood samples — Fajgenbaum learned that his mTOR signaling pathway was over-activated and therefore a potential drug target. He then searched for FDA approved drugs for treating mTOR hyperactivation; sirolimus was one of these drugs. And it worked. Since beginning the experimental treatment seven years ago he has been in full remission. While the drug does not seem to work for all Castleman patients, it has apparently cured a number of others besides Dr. Fajgenbaum. There are now clinical trials in progress to demonstrate efficacy and safety via the usual channels and methods (randomized trials and error-controlled statistical analysis).
But take note: Dr. Fajgenbaum’s initial life-saving discovery 1) did not utilize any statistical hypothesis tests, and 2) neither was it blind luck that he thought to try sirolimus. There was data collection and data analysis and a hypothesis and a very practical test of that hypothesis (self-treatment). I hope we can all agree that this was obviously a scientific investigation. But it wasn’t an RCT and it didn’t have error controlled procedures. What it did have is a putative mechanistic justification (the mTOR pathway) based on previous confirmatory studies in other contexts .
Fajgenbaum’s t-test-free science success story has many, many historical precedents, of course. As Cosma Shalizi writes in his (mostly glowing) review of Deborah Mayo’s “Error and the Growth of Experimental Knowledge”:
“[T]here was lots of good science long before there were statistical tests; Galileo had reliable experimental knowledge if anyone did, but error analysis really began two centuries after his time. (If we allow engineers and artisans to have experimental knowledge within the meaning of the act, we can push this back essentially as far as we please.) If experimental knowledge is reached through severe tests, and the experimenters knew not statistical inference, then the apparatus of that theory isn’t necessary to formulating severe tests.”
Fajgenbaum’s story shows that statistics isn’t necessary for science. Here is story which may help convey that statistical methodology isn’t sufficient either.
In 2010, a small psychology experiment (n=42) was conducted and reported in a peer-reviewed paper. The finding was that “power posing” (standing like Superman, arms akimbo, or like Captain Morgan) has measurable physiological effects: raises testosterone, lowers cortisol, and increases subjective feelings of power. The associated TED talk in 2012 and a subsequent popular science book in 2015 went viral and the idea of power posing entered the business lexicon. Consultants and trial lawyers ate that shit up.
However, in the same year the book came out, additional academic work came out showing that in the meantime the original result didn’t replicate — colleagues repeating the experiment could not reproduce the result. The paper’s first author was sufficiently convinced by the new work to disavowed the theory. Ron Kohavi (whom I paraphrased this timeline from) reports that in the last year the TED talk has received an additional 2.1M views. Kohavi uses this story as a cautionary tale about underpowered studies, noting that the initial study had power of only approximately 6%.
While I think we can all agree that higher powered studies are better than lower powered ones ceterus paribus, I think there were far better reasons to disbelieve the initial study, which is simply that it was a frivolous and implausible hypothesis in the first place. This is what happens, I would argue, when we allow “findings” to be reported as science instead of actual theories. In other words, the power pose research was bad science and also bad statistics, not bad science simply because it was bad statistics. Better power alone wouldn’t (or shouldn’t) have made it an attention-worthy paper.
A defining feature of Tukey’s EDA is that it was “model free” and many people associate it with rank-based analyses. So it may come as a surprise that I advocate for Bayesian machine learning as a modern incarnation of Tukey’s program. The reason I think it works is that, to my mind, the spirit of Tukeyian model-free EDA was primarily about being flexible and robust rather than being model-free per se. Bayesian machine learning can bring both of these qualities, if done with care.
The value-add of going the Bayesian machine learning route is the ability to be systematic about measuring the degree-of-support of which hypotheses to follow-up on, which inevitably must be made, without artificially or arbitrarily limiting the scope of hypotheses under consideration. Subjective priors can frankly be used in this context, while shrinkage/regularization (broadly construed) prevent one from reading too much into the tea leaves. Type I/II error control is too much to ask of an EDA, but we will still want to prevent gross-overfitting and chasing of noise.
Typically, EDA is either ignored (everything is treated like a CDA), or worse, it is done prior to a CDA on the same data set (tsk tsk). Hypothesis generation is treated as a purely intuitive endeavor in which case we call it an art (for other less rigor-minded folks to waste their time with) and leave the serious science for (ourselves) later. To my mind, Bayesian machine learning seems strictly better than any either of these options.
(Of course, lots of Bayesian machine learning is done poorly, but we must not judge an approach by its worst exemplars — if we did that, no one would recommend any form of statistical analysis, ever!)
With this in mind, let’s look at three virtues of Bayesian machine learning for EDA: flexibility, prior information, borrowing of information (analogies)
Flexibility
In my opinion, modern machine learning is best viewed as a massive leap forward in EDA technology. It’s a tool specifically for finding patterns in data. Why wouldn’t we want to use that?
Here is a metaphor to ponder: machine learning is like a microscope.
Widely regarded as one of the major breakthroughs of contemporary science, the invention of the microscope involved no prediction and no control of error rates. Instead, it gave us the ability to see things we simply couldn’t see before. (The analogy may be extended to include all manner of optical augmentation devices — telescopes, X-rays, etc.) Machine learning does the same thing. We cannot “by eye” see if various combinations of dozens of factors show strong associations with some response variable (in our data). But machine learning algorithms can — it’s what they were designed to do.
Like a microscope, ML must be used intentionally. A microscope doesn’t do its thing automatically — we have to prepare the slides and mount them and look through the eyepiece. And decide what to examine. And do follow-up experiments and interpretation. Same is true of machine learning. To avail ourselves of the machine learning “microscope”, studies should be designed explicitly to collect a richer set of environmental and other contextual factors. A commitment to expanding our record keeping would provide the grist for the machine learning mill.
Knowing which factors to record relies — as ever — on the results of previous experiments and theory-laden guesses; there’s no free lunch there. But to make no effort in this direction would be like not using the microscope because it doesn’t come with an instruction manual telling us what to look at with it.
This vantage point nicely captures, I think, Breiman’s advocacy for machine learning methods in his famous “Two Cultures” paper. The value of machine learning over parametric statistical models is that they are able to accommodate and reveal unanticipated patterns.
Regularization
This is not to say, of course, that exploratory analyses should be held to no standards – that would invite overwhelming the literature with chance associations (albeit in the name of “hypotheses” rather than “findings”). While I regard the derision with which some statisticians greet claims of “marginal significance” as a counterproductive form of bullying, the methodological anarchism of mainstream bioinformatics and digital medicine is a bridge too far. Just because your algorithm made a pretty picture doesn’t mean that the science is done. One, you want some kind of notion of uncertainty associated with that pretty picture — we do, after all, have to weigh our opportunity costs when deciding what leads to follow-up on. And two, that follow-up ought to involve a more buttoned-down and narrower confirmatory study.
The Bayesian framework is ideal for conducting flexible pattern discovery while reigning in the risk of over-fitting with regularization priors. Moreover, the regularization can be imposed in subtle ways. For example, it can be used to bias estimates towards particular values such as biasing an average treatment effect estimate towards zero (no effect) or towards the values of previous studies, but it can also be used to impose bias towards structures, such as “shrinking” towards homogeneity or additivity. We can fit a nonlinear model but bias towards a linear model, or fit a model with either additive or multiplicative errors, but bias towards additivity. We can permit higher-order interactions if the data strongly suggest it, but explicitly pre-register a “preference” towards a model with only main effects.
Additionally, the Bayesian framework yields uncertainty quantification, meaning that our microscope clearly indicates its resolution on the console, informing us of its own limits. What to do with ambiguous posteriors is not necessarily straightforward, but the alternative is what, to not use our pattern discovery machine when formulating our hypotheses and to not query that machine’s reported resolution?
In summary, my sales pitch is this: careful Bayesian machine learning can incorporate statistical uncertainty to EDA in a principled way, fully marshaling the available data without inciting wild-goose chases.
Borrowing information
A particular strength of Bayesian statistics in an exploratory (flexible, empirical, hypothesis generation) context is its ability to allow analogical data analysis. That is, via informative prior distributions over our data generating process, we can intentionally inject information from previous studies not directly related to the present data set.
For instance, when trying to infer the reproduction number describing the covid-19 pandemic, one might want to acknowledge that it is a respiratory virus from a family that we had previously studied. One of my major frustrations with the scientific establishment’s treatment of these questions during the pandemic was the pretense that covid-19 was entirely sui generis — entirely without precident — when in fact there were many analogies with other virus, including the common flu, that ought to have reasonably informed our decision-making.
This sort of analogy-based reasoning plays an important role in scientific inquiry — new drugs are similar to old drugs, new treatments are similar to previous treatments, new learning strategies are similar to traditional learning strategies, public policies in one place are similar to other public policies in other places. There is a conceit that serious science is “objective” in the naive sense of beginning with a blank slate at each analysis. But this is neither an accurate portrayal of science nor a desirable one. We want our knowledge of the world to compound, and using earlier investigations to steer the course of our future directions is not only licit, but advantageous. During confirmatory science, we can disregard our biases to get a “pure” measure of evidence, but to ignore those hard-earned biases during our exploratory phase is simply inefficient use of information.
Pharmacometrician James Rogers writes: “The discipline of statistics tends to be very focused on design and analysis methodologies, and the methodology of scientific argumentation involves more than just design and analysis. Scientific argumentation also involves consideration of multiple lines of evidence, holding them in tension, evaluating how they do or don’t corroborate each other, triangulating the truth (more or less: what belongs in the Discussion section of a scientific paper). In my experience, statistical training doesn’t put a lot of emphasis on that part of the scientific process, and that’s where “hints” and “marginally significant” results can be particularly important. “Hints” are rightly down-weighted when definitive statistical confirmation is on the line, but there is a lot more to science than just confirmation. “
Bayesian statistics — specifically nonparametric Bayesian models — is basically ideally designed to do what Rogers describes.
Frankly, I have something of a hard time understanding why anyone would object to this framing. The choice isn’t between error-controlled frequentist hypothesis testing and Bayesian machine learning. I’m happy to abide by the orthodox rules of statistical significance before declaring any particular finding trustworthy. The choice, rather, is at the hypothesis generation phase, and it’s a choice between raw intuition and intuition guided — disciplined, informed, and augmented — by Bayesian (machine learning) data analysis.
For more on Popper and Bayesian statistics, please read the excellent paper by Gelman and Shalizi, which I read many years ago and revisited closely in preparing this essay.



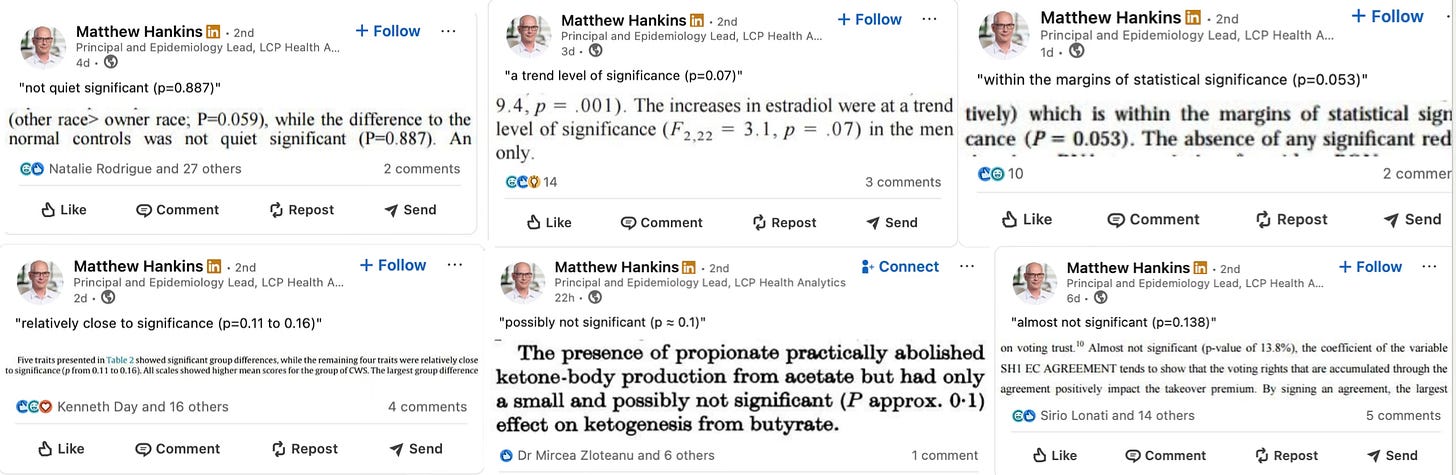


I was under the impression the joke was about the arbitrariness of the 0.05 threshold, not bullying. That's good to know, not acceptable.